Xin giới thiệu đến các bạn một số điều hữu ích về số nhị phân mà mình đã từng đọc trong cuốn Write Great Code - Volume 1. Understanding the Machine của tác giả Randall Hyde. Đây cũng là một quyển sách khá hay mà các bạn có thể đọc để trau dồi thêm kiến thức.

Mục lục

1. Hệ nhị phân

Một số có thể được biểu diễn trong hệ nhị phân bằng 2 chữ số 0 và 1 (thay vì 10 chữ số từ 0 đến 9 đối với hệ thập phân). Hầu hết các máy tính hiện nay đều tính toán trên hệ nhị phân. Do đó, những giá trị và những đối tượng cũng được biểu diễn dưới dạng nhị phân. Các máy tính không thể biểu diễn một giá trị nhị phân tùy ý mà chỉ có thể biểu diễn giá trị với một kích thước nhất định.

Trong máy tính, các giá trị nhị phân được biểu diễn dưới dạng các bit. Một bit biểu diễn 2 giá trị khác nhau, có thể là 0 hoặc 1, đúng hoặc sai, có hoặc không, …

Các bit kết hợp với nhau sẽ tạo thành một chuỗi bit. Chúng ta có các chuỗi bit sau:

• Nibble: Chuỗi 4 bit. Hầu hết các máy tính không hỗ trợ truy cập 1 nibble trong bộ nhớ.
• Byte/Octet: Chuỗi 8 bit. Là đơn vị nhỏ nhất mà các máy tính có thể truy cập vào bộ nhớ. Do vậy, hầu hết các ngôn ngữ lập trình hỗ trợ kiểu dữ liệu nhỏ nhất là 1 byte. Octet được sử dụng khi thuật ngữ byte có ý nghĩa mơ hồ, vì byte trong lịch sử từng được sử dụng làm đơn vị lưu trữ có nhiều kích thước khác nhau (không chỉ là 8 bit).
• Word: Chuỗi 16 bit.
• Double word: Chuỗi 32 bit.
• Quad word: Chuỗi 64 bit.
• Long word: Chuỗi 128 bit.
• Tbyte: Chuỗi 80 bit. Sử dụng trong các hệ CPU Intel 80x86 để giữ các giá trị chấm động và các giá trị BCD nhất định (BCD - binary-coded decimal là một giá trị thập phân được mã hóa nhị phân).

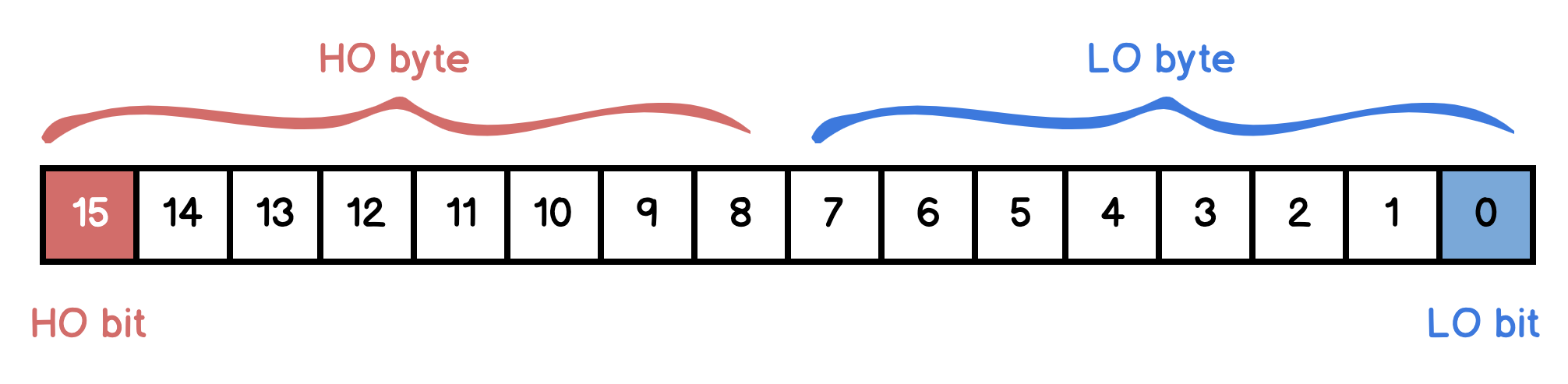
Khi biểu diễn một chuỗi bit, ta sẽ đánh dấu các bit từ phải qua trái và bắt đầu từ 0. Bit bên phải cùng ứng với bit vị trí thấp nhất gọi là bit LO (low-order), bên trái cùng là bit HO (high-order). Cũng dùng LO để chỉ vị trí từ bên phải qua và HO cho vị trí từ bên trái qua.

Minh họa một chuỗi 16 bit

2. Những đặc trưng thú vị khi biểu diễn số nhị phân trong máy tính

1. Nếu bit LO của số nhị phân (số nguyên) là 1 thì số đó là số lẻ. Ngược lại, nếu là 0 thì là số chẵn. Ví dụ: Cho số nhị phân 00110101, nhìn bit LO là 1 thì có thể đoán ra ngay đây là số lẻ.

2. Nếu một lượng n-bit LO đều là 0, thì số đó có thể chia hết cho 2ⁿ. Ví dụ: Với số nhị phân 01010000, 4-bit LO đều là 0 nên số này có thể chia hết cho 2⁴.

3. Nếu số nhị phân có bit thứ n là 1, tất cả các bit còn lại là 0 thì số đó bằng 2ⁿ. Ví dụ: số nhị phân 00010000, chắc chắn số này bằng 2⁴.

4. Nếu n-bit LO đều là 1, các bit còn lại là 0, thì số đó bằng 2ⁿ - 1. Có thể nói là 2ⁿ - 1 sẽ chứa n bit đều là 1.

5. Dịch trái 1 bit toàn bộ các bit trong số nhị phân sẽ tương đương với phép nhân với 2.

6. Dịch phải 1 bit của số nhị phân không dấu tương đương với phép chia cho 2 (phần lẻ sẽ được làm tròn xuống). Không áp dụng với số nguyên có dấu.

7. Nhân 2 giá trị nhị phân n-bit có thể cần 2n bit để lưu kết quả.

8. Cộng hoặc trừ 2 số nhị phân n bit sẽ không cần quá n + 1 bit để lưu.

9. Đảo tất cả các bit của số nhị phân sẽ tương đương với đổi dấu một số nguyên ở hệ thập phân và trừ đi 1. Phép toán đảo bit sẽ đảo bit 0 thành 1 và 1 thành 0. Vì vậy, số nhị phân 00001001 ở hệ thập phân là 9 khi đảo tất cả các bit thành 11110110 thì giá trị của nó sẽ là -10. Lưu ý là ở đây mình đang minh họa giá trị ở dạng số nhị phân 8-bit nhé. Nếu các bạn có số nhị phân 16-bit 0000000000001001 biểu diễn số 9, thì khi đảo bit lại là 1111111111110110 mới biểu diễn số -10.

10. Tăng giá trị của số nguyên nhị phân không dấu lớn nhất thêm 1 sẽ luôn cho kết quả là 0. Điều này cũng dễ hiểu, giả sử bạn có số nguyên không dấu 8-bit lớn nhất là 11111111 biểu diễn số 255, nếu thêm 1 vào sẽ là 100000000 (9 bit) biểu diễn số 256. Vì số nguyên này chỉ biểu diễn được 8 bit, nên sẽ thành 00000000. Các bạn sẽ thấy kiểu dữ liệu 1 byte không dấu thường chỉ biểu diễn được từ 0 đến 255 mà thôi.

11. Trừ giá trị của số nguyên nhị phân không dấu đi 1 sẽ luôn cho kết quả là số nguyên nhị phân không dấu lớn nhất.

12. Một giá trị n-bit sẽ cho ra 2ⁿ các kết hợp duy nhất của các bit. Ví dụ: Số nhị phân 8-bit sẽ cho ra 2⁸ giá trị duy nhất, tức là biểu diễn được 256 giá trị.

3. Các phép toán thú vị

Các phép toán bitwise (AND, OR, NOT, SHIFT LEFT, SHIFT RIGHT,… ) có thể hữu dụng để tính toán nhanh trong một số tình huống thường gặp:

3.1. Kiểm tra 1 bit bên trong dãy bit dùng phép toán AND

Tình huống hay gặp nhất là kiểm tra bit cuối cùng để xác định chẵn hay lẻ. Chúng ta cần tạo ra một mask để thực hiện việc này. Bit cuối cùng của mask sẽ là 1 và các bit còn lại là 0. Phép toán AND sẽ biến các bit khác thành 0, ngoại trừ bit cuối cùng. Nếu bit cuối cùng là 0 sẽ dẫn đến kết quả là 0, còn nếu là 1, phép AND sẽ không thay đổi giá trị của nó.

Mã giả như sau:

// biến `a` là biến cần test
result = (a & 1) != 0;

Vậy trong trường hợp bit mà bạn muốn kiểm tra không phải là bit cuối cùng thì sao? Chỉ đơn giản là dời bit đó về cuối cùng thông qua phép dịch phải, rồi thực hiện phép toán AND với mask. Mask của chúng ta ở đây là 1.

// cần test bit thứ `n` của biến `a`, n bắt đầu từ 0 nhé
result = ((a >> n) & 1) != 0;

Hoặc một cách khác là:

// cần test bit thứ `n` của biến `a`
result = (a & (1 << n)) != 0;

3.2. Kiểm tra 1 chuỗi n-bit dùng phép toán AND

Tương tự với trường hợp kiểm tra 1 bit, bạn có thể kiểm tra một chuỗi n-bit có phải toàn là 0 hay không bằng cách tạo ra 1 mask với toàn giá trị 1, rồi dùng phép toán AND để kiểm tra.

Ví dụ: Bạn muốn kiểm tra 4-bit cuối có phải toàn là 0 hay không?

Nếu biết giá trị của mask 1111 là 15, bạn có thể dễ dàng làm như sau:

// biến `a` là biến cần test
result = (a & 15) != 0;

Nếu không biết giá trị của mask mà bạn muốn tạo một mask n-bit, có thể làm như sau:

mask = (1 << n) - 1;

Giả dụ n = 4, bạn có 1 << 4 sẽ là 10000, trừ đi 1 thì mask của bạn sẽ là 1111.

Vậy có thể kiểm tra chuỗi n-bit như sau:

// biến `a` là biến cần test chuỗi `n` bit cuối cùng
result = (a & ((1 << n) - 1)) != 0;

Thật đơn giản phải không nào!