Box and Whisker Plot (còn gọi là Boxplot) là một dạng biểu đồ hay được dùng trong khoa học dữ liệu và thống kê. Trong bài này chúng ta cùng khám phá về Boxplot và một số điểm thú vị của loại biểu đồ này.

Mục lục

1. Boxplot là gì?

Boxplot là một dạng biểu đồ thể hiện phân phối dữ liệu của các thuộc tính số thông qua các “tứ phân vị” và được giới thiệu lần đầu bởi John Tukey vào năm 1970.

Tứ phân vị là một khái niệm trong thống kê dùng để mô tả sự phân bố và sự phân tán của tập dữ liệu, gồm 3 giá trị: $Q_1$, $Q_2$ và $Q_3$ chia tập dữ liệu thành 4 phần bằng nhau.

Boxplot thể hiện các phân phối dữ liệu, nghĩa là giúp chúng ta biết được độ dàn trải của các điểm dữ liệu như thế nào, dữ liệu có đối xứng không, phân bố rộng hay hẹp, giá trị nhỏ nhất, lớn nhất và các điểm ngoại lệ.

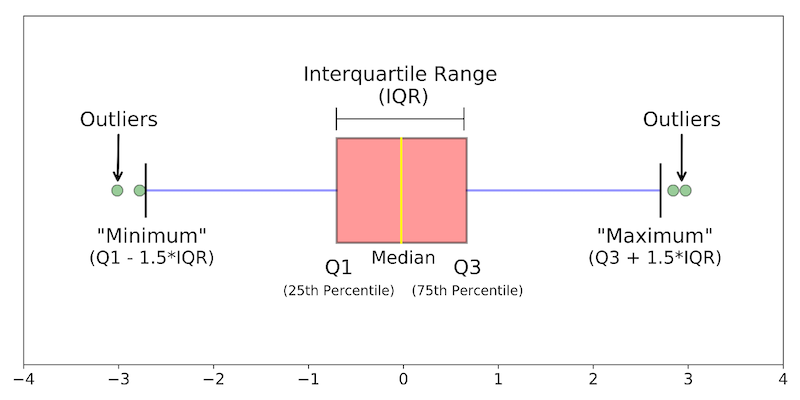
Biểu đồ Boxplot thể hiện 5 thông số:

• Median: Trung vị của tập dữ liệu, tức là giá trị ở phần tử giữa.
• First quartile (Q1): Trung vị giữa Median và phần tử nhỏ nhất trong tập dữ liệu. Còn gọi là 25th Percentile.
• Third quartile (Q3): Trung vị giữa Median và phần tử lớn nhất trong tập dữ liệu. Còn gọi là 75th Percentile.
• Minimum: Phần tử nhỏ nhất không phải ngoại lệ.
• Maximum: Phần tử lớn nhất không phải là ngoại lệ.

Ví dụ cụ thể trong phần sau sẽ giúp hiểu hơn về cách vẽ Boxplot từ dữ liệu.

2. Trình bày dữ liệu dùng Boxplot

2.1. Vẽ Boxplot

Ví dụ sau sẽ giúp các bạn hiểu rõ về cách xây dựng Boxplot.

VD: Một nhà hàng ghi lại khoảng cách từ khách hàng đi từ nhà đến nhà hàng như sau: 24, 10, 23, 11, 21, 22, 23, 15, 23, 21, 23, 23, 22, 24, 24, 10, 24, 25, 27, 27, 19

Trước tiên để tìm được các số liệu để vẽ Boxplot cần sắp xếp lại dữ liệu:

10, 10, 11, 15, 19, 21, 21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 24, 25, 27, 27

Dữ liệu có 21 phần tử nên trung vị của nó là phần tử thứ 11 (Trường hợp số phần tử là chẵn thì trung vị sẽ là giá trị trung bình của 2 phần tử đứng giữa).

Nên ta có $ Median = 23 $.

First quartile sẽ là trung vị của các điểm dữ liệu bên trái Median. Vậy Q1 sẽ là median của các điểm:

10, 10, 11, 15, 19, 21, 21, 22, 22, 23

nên $Q_{1} = \frac{19+21}{2}=20$

Tương tự, Q3 là trung vị của các điểm dữ liệu bên phải Median.

23, 23, 23, 24, 24, 24, 24, 25, 27, 27

nên $Q_{3} = \frac{24+24}{2}=24$

Với Boxplot không thể hiện ngoại lệ, Minimum và Maximum sẽ là giá trị nhỏ nhất và lớn nhất.

$$Minimum = 10$$ $$Maximum = 27$$

Từ các thông số trên, bạn sẽ vẽ được:

2.2. Ngoại lệ

Trong thống kê, một ngoại lệ (outlier) là một điểm dữ liệu khác biệt đáng kể so với các quan sát khác. Một ngoại lệ có thể là do sự thay đổi trong phép đo hoặc là lỗi và thông thường được loại trừ khỏi tập dữ liệu bởi nó có thể gây ra vấn đề nghiêm trọng trong phân tích thống kê.

Để tìm ngoại lệ, ta dùng thêm khái niệm IQR.

IQR (Interquartile Range) là một khái niệm trong thống kê mô tả, dùng đo lường độ phân tán của dữ liệu và được tính toán bằng công thức:

$$IQR = Q_{3} - Q_{1}$$

Điểm ngoại lệ sẽ là những điểm nhỏ hơn $Q_{1} - 1.5IQR$ và lớn hơn $Q_3 + 1.5IQR$.

Với ví dụ trước, ta có $IQR = 4$. Vậy các điểm ngoại lệ sẽ nhỏ hơn 14 và lớn hơn 30.

Như vậy ta xác định được Minimum mới và Maximum mới như sau:

$$Minimum = 15$$ $$Maximum = 27$$

Ta vẽ lại được Boxplot vs các điểm ngoại lệ như sau:

Để có sự so sánh giữa thông tin mà Boxplot thể hiện với dữ liệu thực tế, chúng ta có thể xem phân bố điểm dữ liệu như sau:

3. Đọc hiểu Boxplot

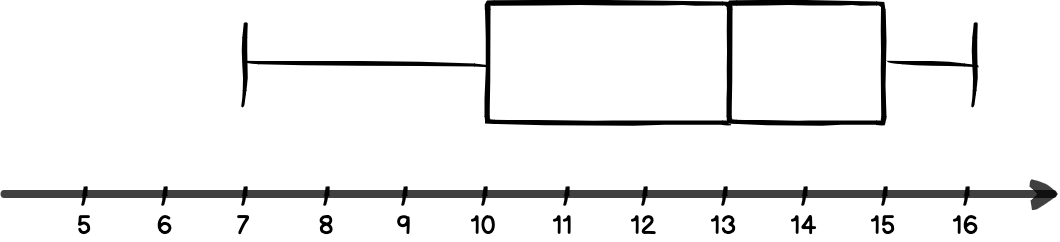
Cho ví dụ sau: Phân bố độ tuổi của các học sinh tham dự buổi tiệc được mô tả bằng Boxplot như bên dưới:

Từ hình ta có thể rút ra một số dữ kiện sau:

• Độ tuổi nhỏ nhất là 7 tuổi.
• Độ tuổi lớn nhất là 16 tuổi.
• Median là 13 tuổi.

Cùng xem xét các khẳng định sau đây:

• Tất cả các sinh viên nhỏ hơn 17 tuổi. Khẳng định này ĐÚNG, vì độ tuổi cận trên là 16 tuổi.
• Ít nhất 75% học sinh từ 10 tuổi trở lên. Từ 7 đến 10 tuổi được gọi là Q1, chiếm 25% số lượng mẫu, nên độ tuổi từ 10 trở lên sẽ chiếm 75% nên khẳng định này ĐÚNG.
• Đúng một nửa số học sinh từ 13 tuổi trở lên. Độ tuổi 13 nằm ở điểm trung vị, nhưng chưa đủ để khẳng định đúng một nửa số học sinh từ 13 tuổi trở lên vì số lượng học sinh 13 tuổi có thể nhiều hơn 1 người. Nên khẳng định này chưa biết đúng sai, khẳng định đúng là: Ít nhất một nửa số học sinh từ 13 tuổi trở lên.
• Có 1 học sinh lớn tuổi nhất là 16 tuổi. Boxplot không thể hiện số lượng mẫu có giá trị lớn nhất và nhỏ nhất. Do đó khẳng định này chưa thể xác định đúng sai.

4. Vẽ Boxplot trong Python

Qua các phần trên, chúng ta đã nắm được cách vẽ và trình bày dữ liệu với Boxplot. Thực tế hầu hết các công cụ khi làm thống kê và khoa học dữ liệu đều đã hỗ trợ vẽ Boxplot một cách tự động.

Bên dưới là một ví dụ về Boxplot được vẽ bằng thư viện Seaborn với ngôn ngữ Python.

import matplotlib.pyplot as plt 
%matplotlib inline 
import seaborn as sns

tips = sns.load_dataset("tips")

sns.boxplot(x="day", y="total_bill", hue="smoker",
                 data=tips, palette="Set3")

Kết quả:

5. Kết luận

Bài viết đã giới thiệu tổng quan về Boxplot và cách dùng nó để biểu diễn dữ liệu. Hi vọng sẽ giúp ích cho các bạn trong quá trình học tập, làm việc.

Tham khảo

• Khan Academy: Box and Whisker plot
• Box and Whisker Plot
• Box plot
• seaborn.boxplot